DATA 420 - Modeling and Simulation - Spring 2024
Possible experience: +40XP (or even +60XP or even +80XP)
Due: Friday, April 5, midnight
In this homework, you'll be implementing an agent-based epidemiology model that relaxes the mean-field assumption of the SIR and similar compartment-based models.
Create Model and Agent classes to represent this spatially-based model. Each agent should be, at any point in time, in one of three states: SUSCEPTIBLE, INFECTED, and RECOVERED. Agents should initially be placed randomly on a square grid, with no more than one agent per cell. All the agents, except one, should start out in the SUSCEPTIBLE state. (The remaining one starts out INFECTED.)
Agents should move randomly to an adjacent square (Von Neumann neighborhood with radius 1) every clock tick. Any time a SUSCEPTIBLE agent is in an adjacent square to an INFECTED agent, the disease should be passed from former to latter. (In rare cases, this could even result in a single infected agent transmitting the disease to multiple susceptible agents in the same iteration, if the timing and movement worked out.)
Once infected, agents will stay infected for a fixed number of clock ticks, after which they will move to the RECOVERED state permanently. (Hint: you'll need to add a variable to the Agent's purple box — an inst var, for those who have had OOP before — to represent how long each infected agent has been infected.)
Your code should display an animation of the agents interacting, with cells drawn in a different color for each of the three states.

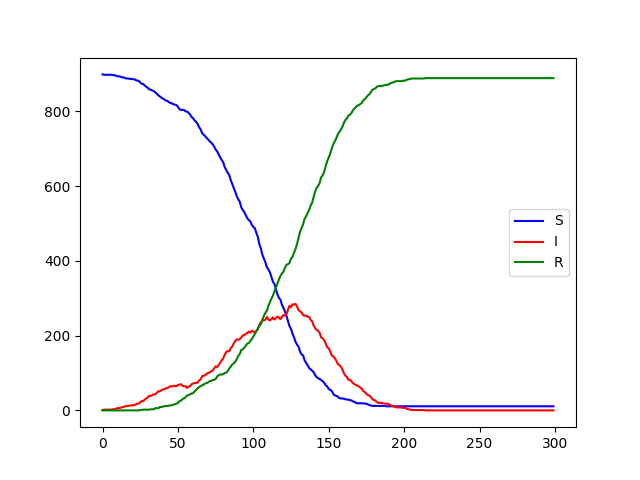
You should also write code to produce the same sort of time-series plot that we had for the system dynamics version of the SIR model:
Add code to run your code in a parameter-based way, so that you can run it many times for given parameter choices, and so that you can run a selected parameter through a range of values. Your parameters (independent variables) should include:
Also write code to gather data about each run of your model. Specifically, the dependent variables you collect should include:
Produce a plot showing independent variable #3 on the x axis and dependent variable #2 on the y axis.
Add states, and the requisite code, for vaccinated and dead agents. Add this to the animation. Note: vaccinated agents move just like non-vaccinated ones. However, dead agents no longer move.
Down the middle of the grid, splitting it vertically into equal left- and right- halves, create a wall. (This will consist of a column of cells that agents cannot enter.) Turn off the grid's torus (so agents can no longer wrap around the border to the other side of the globe, Pac-man style). Add the wall to your animation in some reasonable way so it can be seen. Run the simulation and verify that only agents on the side of the wall with the initial infected agent can ever get infected.
Now, create a hole in the middle of the wall, which can be of varying length, anywhere from zero cells long (a solid wall) to the entire grid's height (no wall at all). Treat the size of the hole as an independent variable, and produce a plot showing the size of the hole on the x axis and dependent variable #2 on the y axis.
It's okay, and perfectly understandable (and even encouraged, in a way) to look at the Boltzmann model we did in class as you write this program. But I encourage you not to try and start with Boltzmann and progressively morph it into SIR. Instead, I encourage you to learn from the Boltzmann program the lessons that are worth learning, and to write the SIR program from scratch, with those principles in mind.
Send an email to data420submissions@gmail.com containing attachments for all the work you've done. This should include:
The subject line of this email should be "DATA 420 ABM II turnin".
Come to office hours, or send me email with subject line "DATA 420 ABM II help!!"